Meu primeiro código Python, 14 anos depois

Ao folhear alguns de meus backups antigos, me deparei com algumas das primeiras coisas que eu escrevi em Python. Foi em 2007, enquanto eu cursava a graduação em Matemática Computacional, que eu estudei fundamentos de criptografia na universidade com o professor Dr. Jeroen van de Graaf, no Departamento de Ciência da Computação da Universidade Federal de Minas Gerais. Para os exercícios de aprendizagem, nós precisávamos fazer cálculos com grandes números inteiros, algo que não era simples de se fazer em muitas das linguagens de programação da época. O Prof. Jeroen sugeriu que usássemos Python para isso, o que acabou facilitando muito traduzir em código executável os algoritmos abstratos dos livros.

Nós usamos muitos livros sobre teoria dos números e criptografia, mas aquele ao qual recorríamos com mais frequência era o “Manual de Criptografia Aplicada” (“Handbook of Applied Cryptography”), de Menezes, Oorschot e Vanstone, muitas vezes abreviado para “HAC”. Muitos dos algoritmos que implementamos no curso são descritos nesse livro.

O estado do Python era bastante diferente na época, pois a linguagem evoluiu muito ao longo dos anos. Acho que eu usava a versão 2.3 do Python. Na época usar o operador de divisão / em inteiros retornava inteiros. Agora você recebe um float em vez disso. Então no Python 3 você tem que usar a barra dupla // para a divisão inteira se quiser que o resultado seja um int.

Além disso, a minha própria inexperiência com a linguagem está evidente nesse código. Salta aos olhos que estou tentando imitar algumas estruturas da linguagem C em diversos lugares. Por exemplo, eu usei um loop for exatamente como alguém o faria em C, que é algo ao qual eu estava acostumado a fazer na época, em vez de iterar em uma lista.

for i in range(0 , t) :
    a = numeros[i]
# em vez do pythônico
for a in numeros[:t]:
    ...

Por outro lado, me traz um sorriso ver um cabeçalho especificando a licença GPL 2 para o código. A minha admiração e o meu compromisso pela ideia do software livre vêm de longa data.

O que eu implementava então? Não tenho certeza de qual exatamente eu fiz primeiro, porque os timestamps de modificação do arquivo estão errados – eles foram atualizados em uma operação anterior de backup, mas com certeza é um destes. O código abaixo tenta implementar o teste de primalidade de Miller-Rabin para determinar se um número é composto ou provavelmente primo. Não vou mostrar o código original, pois ele está implementado de forma completamente errada. O Miller-Rabin é um teste probabilístico, e assim começa com a escolha de um número aleatório \(a\), onde \(2 \leq a \leq n - 2\). No exercício, eu havia usado uma lista fixa de números em vez disso. E esse é apenas um de vários erros.

Se você estiver curiosa(o) sobre como funciona o teste de Miller-Rabin, aqui está uma versão corrigida (assim espero) da minha implementação do algoritmo que está descrito no Capítulo 4 do HAC:

from random import randint
from colorama import Fore

def is_prime_MR (n: int, t: int) -> bool:
    """Verifica se um número é composto ou provavelmente primo,
    usando o teste probabilístico de Miller-Rabin.

    :param int n: O inteiro a ser testado
    :param int t: Parâmetro de segurança, números maiores demoram
                  mais, mas aumentam a probabilidade do número ser
                  primo

    :return: False se o número é composto, True se primo ou pseudoprimo
    :rtype: bool
    """
    if (n % 2 == 0) : return False
    r = n - 1
    s = 0
    while (r % 2 == 0):
        s = s + 1
        r = r // 2
    for i in range(t):
        a = randint(2, n - 2)
        y = pow (a, r, n)
        if (y != 1) and (y != n - 1):
            j = 1
            while (j < s) and (y != n - 1):
                y = (y * y) % n
                if y == 1:
                    return False
                j = j + 1
            if y != n - 1:
                return False
    return True

# testa números de 4 a 400 com 10.000 iterações cada
numbers = ' '.join(
    (Fore.RED if is_prime_MR(n, 10000) else Fore.WHITE) + f'{n:3}'
        for n in range(4, 401)
)

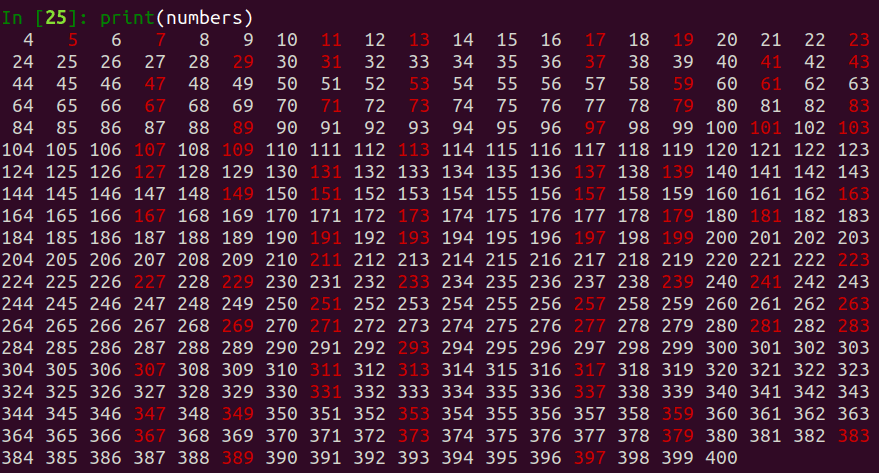
Eu também implementei o algoritmo Pollard Rho para factoração e para encontrar logaritmos discretos, conforme descrito no HAC, Capítulo 3. Percebe-se imediatamente o uso extensivo de funções lambda, o que é interessante porque:

• ajudam muito na implementação de algoritmos matemáticos como este, e
• já estavam presentes nesta jovem etapa da história do Python.

Para o máximo divisor comum, usamos a versão contemporânea do numbthy.py do Robert Campbell, que é simples e útil para aprender, mas hoje em dia provavelmente se daria preferência a importar a função para MDC do numpy que é calculada em C e teria um desempenho melhor. Entretanto, mesmo com um computador de hoje em dia ainda não consegui encontrar um fator do número composto 8834884587090814646372459890377418962766907, depois de uma hora de cálculo. Talvez se eu tivesse gasto esforços para paralelizar o algoritmo para aproveitar as CPUs multi-core de hoje em dia, mas não fiz isso. Para o número menor 618240007109027021, por outro lado, ele encontra o fator 250387201 quase que imediatamente. O código abaixo foi atualizado para o Python 3, e eu desaconselho que você o utilize, já que ainda pode conter erros. Mas, se insistir, por favor prossiga com cuidado:

from numpy import gcd

def prho_factor (n: int) -> int:
    """Fatora um número composto n que não é uma potência de um
    número primo.

    :param int n: Um número composto n

    :returns: Um fator não trivial d de n
    """
    a = b = 2
    while True:
        g = lambda x : (x * x + 1) % n
        a, b  = g(a), g(g(b))
        d = gcd (a - b, n)
        if (d > 1) and (d < n):
            return d
        if d == n:
            break

No fim, foi muito interessante tanto revisitar esses algoritmos da teoria dos números quanto relembrar o início da minha jornada pessoal em aprender Python. De acordo com os metadados em um documento de texto OpenDocument, estes códigos estão completando agora o seu 14º aniversário. 🎂 Viva!

Isso significa que esta é a marca do início do meu 15º ano com Python. E ainda aprendo coisas novas todos os dias. Mal posso esperar pelo prazer de aprender mais Python neste próximo ano.